Special Angles and Trig Functions

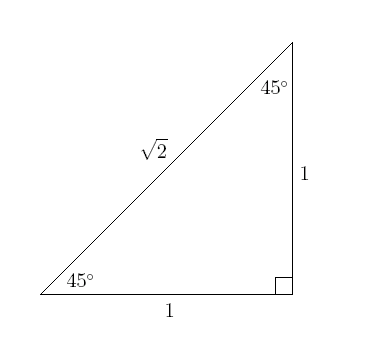
Today in class we learned about special angles and trig functions. We learned that cosecant or cscθ is the inverse of sinθ, secant or secθ is the inverse of cosθ and that cotangent or cotθ is the inverse of tanθ. We also learned about special angles which are most angles on the unit circle that are based off of 30°, 45°, or 60°, and so on. To be able to find the values of these angles as they relate to sinθ, cosθ, and tanθ we had to learn about reference triangles so we can then determine the ratios of the trig functions. We specifically looked at a right angle isosceles triangle which consists of two 45° angles and one 90° angle with sides a and b equal to 1 unit, and an equilateral triangle with the side consisting of 2 units, which was then bisected so we could make two right angle triangles to have the special angles of 30°, 60°, and of course 90°. From these triangles we were able to find the appropriate ratios for the trig functions by using some of the special angles.

For example when given an angle of 45°, what would sin45° =?So to solve for this question we would take a look at the right angle isosceles triangle, which was known to have two 45° angles and sides a and b = 1 unit. So we would need to find side c or the hypotenuse in order to solve for the value of sinθ because we know sinθ= O/H. So to get the hypotenuse we must use Pythagorean theorem, and then will be able to use the trig ratios to solve for sinθ.