Graphing Reciprocal Functions 1

Today in class, we learned about Graphing Reciprocal Functions.


  Basic Shape: ƒ(x) = 1/x            Shifted Shape: ƒ(x = (1/x-h ) + k       

• There will be an asymptote at the value for x that makes the function undefined - this is called a vertical asymptote. In basic form the VA is always at x = 0
• There will also be an asymptote at the value for y that is no longer able to occur due to the unacceptable value for x (VA) - this is called a horizontal asymptote. In basic form, the HA is always at y = 0.
• If the graph is shifted, read horizontal shifts (H values) as opposite of what is given and vertical shifts (k values) as is. Even though there is no bracket around the x - h, act as if there is!
• If the graph is shifted, the VA will always be at x = h and the HA will always be at y = k.
• To sketch we need to have at least three points on either side of the VA.
• Remember to find x-intercept -- make y = 0 and solve for x.
• Remember to find y-intercept -- make x = 0 and solve for y.
• If a negative is placed in front of the function, this means to multiply all of your y-values by -1.

Example:

1. ƒ(x) = 1/x

                2. ƒ(x) = -1/x

          


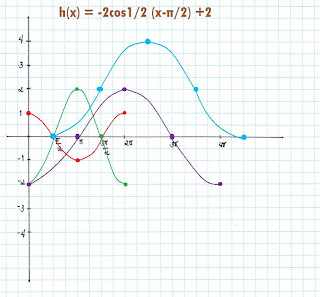
Mr. P also did the graph of h(x) = -2cos1/2 (x- π/2) + 2 [blue]


He did it step by step (:

• first, he graphed the function h(x) = cos(x) [red]
• then he multiplied the y-values by -2 [green] 
• then he multiplied the x-values by 2 [purple]
• then he shifted the [purple] function to the right by π/2 and moved it up by 2 [blue]

                  

♥