
Graph of a Natural Logarithms
Definition of Natural Logarithm
When
e y = x
Then base e logarithm of x is
ln(x) = loge(x) = y
The e constant or Euler's number is:
e ≈ 2.71828183
Common Logarithms use the Base 10Natural Logarithms use the Base e
Note:
All Natural Logarithms use the same laws and patterns as Common Logarithms
Division - Subtraction
Multiplication - Addition
Exponents - Move to the front
Same Base - Cancel
Change of Base - use e instead of 10
Natural logarithm rules
Product:
The rule name is product. The rule is,
logx (a.b) = logx a + logx b.
The example is,
logx (9.8) = logx 9 + logx 8.
Quotient:
The rule name is quotient. The rule is,
Log (a/b) = loga – logb.
The example is,
Log (10/8) = log10 – log8.
Change of base formula:
The rule name is change of base formula. The rule is
Log ab = logb /log a.
The example is,
Log 8.2 = log8 /log 2.
Power
The rule name is power. The rule is,
ln(a b) = b ∙ ln(a)
The example is,
ln(85) = 5 ∙ ln(8)
Examples
Solve for x

| Divide both sides by 7 | |
| | Use Property of Logarithms, Part 2, to take the log of both sides |
| | Property of Logarithms: |
| | ln e = 1 |
 | Divide both sides by 3 |
| x » 1.266 |

| | |
| | Use Property of Logarithms, Part 2, to take the log of both sides |
| (x + 2) ln 2 = (2x + 1) ln 3 | Property of Logarithms: |
| x ln 2 + 2 ln 2 = 2x ln 3 + ln 3 | Distributive Property |
| x ln 2 - 2x ln 3 = ln 3 – 2 ln 2 | Isolate terms with the variable on one side of the equation |
| x(ln 2 – 2 ln 3) = ln 3 – 2 ln 2 | Factor out the common factor, x |
|
x » 0.191 |




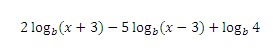





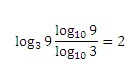





.png)
.png)

.png) and the quadrant where it lies, verifying, finding exact values and expressing the following as function of
and the quadrant where it lies, verifying, finding exact values and expressing the following as function of  .
.
.png) and
and .png) we must identify the other point of the right triangle using the Pythagorean Thereom equation
we must identify the other point of the right triangle using the Pythagorean Thereom equation  . Since
. Since .png) is
is  then...
then...



.png) and
and .png) by using
by using .png) =
=  . Since
. Since  then...
then...



.png)
.png) first. To do so, we must figure out the equation, which is...
first. To do so, we must figure out the equation, which is....png)




.png) . The equation for it is...
. The equation for it is... .png)






