Why there are 360 degrees in circle

One degree (shown in red) and
ninety degrees (shown in blue)

This article describes the unit of angle. For other meanings, see degree.

A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of plane angle, representing¹⁄₃₆₀ of a full rotation; one degree is equivalent to π/180 radians. It is not an SI unit, but can be used with the SI system via the aforementioned π/180 radians conversion.^[1] When that angle is with respect to a reference meridian, it indicates a location along a great circle of a sphere, such as Earth (see Geographic coordinate system), Mars, or the celestial sphere.^[2]

]History

A circle with an equilateral chord (red). One sixtieth of this arc is a degree. Six such chords complete the circle.

The original motivation for choosing the degree as a unit of rotations and angles is not known. One theory states that it is related to the fact that 360 is approximately the number of days in a year.^[3] Ancient astronomers noticed that the stars in the sky, which circle the celestial pole every day, seem to advance in that circle by approximately one-360th of a circle, i.e., one degree, each day. Some ancient calendars, such as the Persian calendar, used 360 days for a year. The use of a calendar with 360 days may be related to the use of sexagesimal numbers.

A alternative theory is that the degree is one sixtieth of the angle of a equilateral triangle. The earliest trigonometry, used by the Babylonian astronomers and their Greek successors, was based on chords of a circle. A chord of length equal to the radius made a natural base quantity. One sixtieth of this, using their standard sexagesimal divisions, was a degree.

Hipparchos seems to have been the first to exploit Babylonian astronomical knowledge and techniques systematically^[4]. Except for Timocharis and Aristillus, he was the first Greek known to divide the circle in 360 degrees of 60 arc minutes (Eratosthenes before him used a simpler sexagesimal system dividing a circle into 60 parts).

The division of the circle into 360 parts also occurred in ancient India, as evidenced in the Rigveda:^[5]

Another motivation for choosing the number 360 may have been that it is readily divisible: 360 has 24 divisors,^[6] including every number from 1 to 10 except 7.^[7] This property has many useful applications, such as dividing the world into 24 time zones, each of which is nominally 15° of longitude, to correlate with the established 24-hour day convention.

Subdivisions

For many practical purposes, a degree is a small enough angle that whole degrees provide sufficient precision. When this is not the case, as in astronomy or for latitudes and longitudes on the Earth, degree measurements may be written with decimal places, but the traditional sexagesimal unit subdivision is commonly seen. One degree is divided into 60 minutes (of arc), and one minute into 60seconds (of arc). These units, also called the arcminute and arcsecond, are respectively represented as a single and double prime, or if necessary by a single and double quotation mark: for example, 40.1875° = 40° 11′ 15″ (or 40° 11' 15").

If still more accuracy is required, current practice is to use decimal divisions of the second. The older system of thirds, fourths, etc., which continues the sexagesimal unit subdivision, is rarely used today. These subdivisions were denoted by writing the Roman numeral for the number of sixtieths in superscript: 1^I for a "prime" (minute of arc), 1^II for a second, 1^III for a third, 1^IV for a fourth, etc. Hence the modern symbols for the minute and second of arc.

Alternative units

See also: Measuring angles

A chart to convert between degrees and radians

In most mathematical work beyond practical geometry, angles are typically measured in radians rather than degrees. This is for a variety of reasons; for example, the trigonometric functions have simpler and more "natural" properties when their arguments are expressed in radians. These considerations outweigh the convenient divisibility of the number 360. One complete turn (360°) is equal to 2π radians, so 180° is equal to π radians, or equivalently, the degree is a mathematical constant: 1° = ^π⁄₁₈₀.

The turn (or revolution, full circle, full rotation, cycle) is used in technology and science. 1 turn = 360°.

With the invention of the metric system, based on powers of ten, there was an attempt to define a "decimal degree" (grad or gon), so that the number of decimal degrees in a right angle would be 100 gon, and there would be 400 gon in a circle. Although this idea was abandoned already by Napoleon, Some groups have continued to use it and many scientific calculators still support it.

An angular mil, which is most used in military applications, has at least three specific variants, ranging from ¹⁄₆₄₀₀ to ¹⁄₆₀₀₀, each approximately equal to one milliradian.

Conversion of some common angles

Units	Values
Turns	0	$\frac{\tau}{12}$	$\frac{\tau}{8}$	$\frac{\tau}{6}$	$\frac{\tau}{4}$	$\frac{\tau}{2}$	$\frac{3}{4}\tau$	$τ$
Degrees	0°	30°	45°	60°	90°	180°	270°	360°
Radians	0	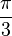$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$	$π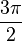$	$\frac{3\pi}{2}$	$2π$
Grads	0^g	33⅓^g	50^g	66⅔^g	100^g	200^g	300^g	400^g