Conics - Circles on Coordinate Plane

In Friday's class, we started a new unit which is the CONICS unit. A circle is the set of all points that are equally distant from a fixed point. The center is the given point, while the radius is a line segment in a circle that has one endpoint at the center of a circle and the other endpoint on the circle. 

NOTE:

STANDARD FORM

x^2 + y^2 = r^2 [if this occurs, the centre will always be at (0,0)]  

OR 

(x - h)^2 + (y - k)^2 = r^2 [center will be at (h,k)]

GENERAL FORM

Ax^2 + By^2 + Cx + Dy + E = 0

HELPFUL FORMULAS:

area of a circle = πr^2 

circumference of a circle = 2πr

distance between two points =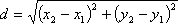 

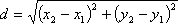
midpoint between two points = 

For example: x^2 + y^2 -6x -10y - 2 is the equation. First thing to do is to rearrange the equation with x's and y's together and what's left goes on the other side. 
(x^2 - 6x) + (y^2 - 10y) = 2  <---- here is the new equation (we used a bracket to separate it)


Next, we take the coefficient, divide by two and then square it. We take "-6" from (x^2 - 6x) and "-10" from (y^2 - 10y): 
(-6/2)^2 = (-3)^2 = 9 
(-10/2)^2 = (-5)^2 = 25


We then add 9 to (x^2 - 6x) and 25 to (y^2 - 10y). We should add 9 and 25 to the other side too and becomes like this: 
(x^2 - 6x + 9) + (y^2 - 10y + 25) = 2 + 9 + 25 
(x^2 - 6x + 9) + (y^2 - 10y + 25) = 36


Lastly, we take the "-3" when we divided it from 6 and "-5" when we divided it from -10 to use to find the center and radius of the conic. 
(x-3)^2 + (y-5)^2 = 6 <---- we take the center and radius from this equation
The center would be the opposite sign for the (x,y) value. Therefore, the center is (3,5). 
To find the radius, we square root "36" from the sum. The radius is 6.
To graph, mark (3,5) as the center. Since 6 is the radius, we move 6 to the left, 6 to the right, 6 up, and 6 down, and make the circle.